But what if there is a net force? Can we predict how the system will move? Consider again our example of a two body system, with m1 experiencing an external force of F1 and m2 experiencing a force of F2. We also must continue to take into account the forces between the two particles, F21 and F12. By Newton's Second Law:
| F1 + F12 | = | m1a1 | |
| F2 + F21 | = | m2a2 |
Substituting this expression into our center of mass acceleration equation we get:
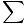 Fext = m1a1 + m2a2 = (m1 + m2)acm
Fext = m1a1 + m2a2 = (m1 + m2)acm
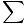 Fext = Macm Fext = Macm |
This equation bears a striking resemblance to Newton's Second Law. In this case, however, we are not speaking of the acceleration of individual particles, but that of the entire system. The overall acceleration of a system of particles, no matter how the individual particles move, can be calculated by this equation. Consider now a single particle of mass M placed at the center of mass of the system. Exposed to the same forces, the single particle will accelerate in the same way as the system would. This leads us to an important statement:
The overall motion of a system of particles can be found by applying Newton's Laws as if the total mass of the system were concentrated at the center of mass, and the external force were applied at this point.
Systems of More than Two Particles
We have derived a method of making mechanical calculations for a system of particles. For simplicity's sake, however, we only derived this for a two- particle system. A derivation for an n particle system would be quite complex. A simple extension of our two particle equations to an n particle system will suffice.
Center of Mass of Many Particles
Previously, M was defined as M = m1 + m2. However, to continue the study of center of mass we must make this definition more general. If there are n particles in a system, M = m1 + m2 + m3 + ... + mn. In other words, M gives the total mass of the system. Equipped with this definition, we can simply state the equations for the position, velocity, and acceleration of the center of mass of a many particle system, similar to the two-particle case. Thus for a system of n particles:
| xcm | = | 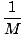 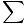 mnxn mnxn | |
| vcm | = | 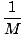 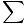 mnvn mnvn | |
| acm | = | 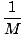 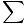 mnan mnan | |
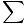 Fext Fext | = | Macm |
These equations require little explanation, as they are identical in form to our two particle equations. All these equations for center of mass dynamics may seem confusing, however, so we will discuss a short example to clarify.
Consider a missile composed of four parts, traveling in a parabolic path through
the air. At a certain point, an explosive mechanism on the missile breaks it
into its four parts, all of which shoot off in various directions, as shown
below.

Such an example displays the power of the notion of a center of mass. With this concept we can predict emergent behavior of a set of particles traveling in unpredictable ways.
We have now shown a way to calculate the motion of the system of particles as a whole. But to truly explain the motion we must generate a law for how each of the individual particles react. We do so by introducing the concept of linear momentum in the next section.


 payment page
payment page



