Dielectric Media
When a light ray impinges on an interface between different media, we saw that some of the light
is reflected from that interface. However, in most cases some proportion of the light enters the second
medium--the light is said to be transmitted. In this section we will concern ourselves only with transparent
or dielectric, media. The main change upon entering different media is that for any dielectric medium,
the permittivity, ε, and the permeability, μ, are different to those in free space. Thus the speed
of light in various media is different: v = 1/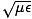 . We define the index of refraction of
the medium as:
. We define the index of refraction of
the medium as:
nâÉá = = 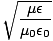 |
Generally substances substances that are transparent are non-magnetic, so μ = mu0, and in this case n =
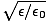 .
.
Of course, this reasoning implies that light can travel faster or slower than c in different media; this seems paradoxical since we have already said that photons can only exist at c. The resolution to this is that light does propagate through the void between the atoms in a medium with speed c, however when it encounters an atom it causes vibrations of the electrons which causes them to act like spherical wave sources. It is these spherical waves which cause the propagation through the medium, and they too travel at c between atoms. However, as you may know from studying driven oscillations, the resulting oscillation usually lags behind the driving oscillation by a factor between 90o and 180o, depending on whether the frequency is above or below resonance. Thus the electron vibrations, and hence the spherical waves, are out of phase with the incident light. As this spherical wave encounters another atom, there will again be a phase-lag for the light emitted from that atom, as so forth. Thus the light propagating through the medium is constantly being retarded (or advanced) in phase. Since we measure the speed of light effectively by watching the motion of a particular crest or trough, the continual phase shift amounts to a macroscopic 'slowing down' of the light.
Refraction
We are now ready to examine what happens to the transmitted ray. To put it simply, light entering a
medium at some non-zero angle with respect to the normal to the surface is bent. That is, upon entering a
different medium, light changes direction. It is not difficult to show that the change of speed involved in
moving from one medium to another implies this change in direction.
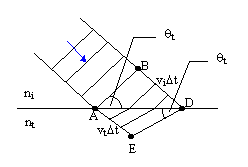
The two right triangles ABD and AED in share a common hypotenuse, AD, so we can write:
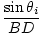 = = 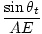 |
But BD = viΔt and AE = vtΔt, so we can write the law of refraction, or Snell's Law as:
| nisinθi = ntsinθt |
where ni = c/vi and nt = c/vt. Moreover, the incident, reflected and refracted rays all lie in the same plane. From Snell's Law it is not hard to deduce that a light ray entering a denser (higher index of refraction) medium bends towards the normal, while a ray entering a rarer (lower index of refraction) medium bends away from the normal. In vector notation, for the normal to the surface
 , and incident and transmitted waves
, and incident and transmitted waves 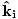 and
and 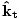 respectively,
the law of refraction can be written:
respectively,
the law of refraction can be written:
ni(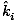 × × ) = nt( ) = nt(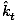 × × ) ) |
Dispersion
We saw that dielectric media have an index of refraction defined by n = 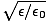 .
For some media, however, this index is dependent on frequency. This effect causes different wavelengths of
light to bend by different amounts upon entering a medium, causing a light beam made up of different colors
to disperse. This phenomenon can be observed when white light enters a prism: the spectral pattern produced
is due to the dependence of the index of refraction of the glass on wavelength (or color). To examine this
effect we must once again consider the oscillations of the electron cloud caused by the oscillating electric
and magnetic fields of the light wave (see the discussion of scattering). It is also possible
that light waves can set up oscillations in ions or polar molecules of a substance, but their much greater
mass means that rapidly oscillating fields have little effect. We can assume that electrons are bound in
atoms in a fashion analogous to a mass on a spring, connecting the electron to the positive nucleus. Such
a system has a natural or resonant frequency σ0 =
.
For some media, however, this index is dependent on frequency. This effect causes different wavelengths of
light to bend by different amounts upon entering a medium, causing a light beam made up of different colors
to disperse. This phenomenon can be observed when white light enters a prism: the spectral pattern produced
is due to the dependence of the index of refraction of the glass on wavelength (or color). To examine this
effect we must once again consider the oscillations of the electron cloud caused by the oscillating electric
and magnetic fields of the light wave (see the discussion of scattering). It is also possible
that light waves can set up oscillations in ions or polar molecules of a substance, but their much greater
mass means that rapidly oscillating fields have little effect. We can assume that electrons are bound in
atoms in a fashion analogous to a mass on a spring, connecting the electron to the positive nucleus. Such
a system has a natural or resonant frequency σ0 =  , where k will be determined by the
strength of the attraction between the electron and the nucleus. The time-varying electric field of the light
ray E(t) will cause a forced oscillation. The force due to this field will be FE = qeE(t) = qeE0cos(σt) where σ is the angular frequency of the light. From
Newton's Second Law we can write:
, where k will be determined by the
strength of the attraction between the electron and the nucleus. The time-varying electric field of the light
ray E(t) will cause a forced oscillation. The force due to this field will be FE = qeE(t) = qeE0cos(σt) where σ is the angular frequency of the light. From
Newton's Second Law we can write:
qeE0cosσt - kx = me = qeE0cosσt - meσ2x = qeE0cosσt - meσ2x |
You can check that the solution to this differential equation is x = x0cosσt. We can substitute this back into the equation to solve for x0 and we find:
x(t) =  E0cosσt E0cosσt |
Now, when a dielectric medium is subjected to an applied electric field,
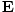 , the internal charge
distribution is altered, creating a dipole moment. In other words, the
external field separates positive and negative charges, creating an additional electric field called
the electric polarization,
, the internal charge
distribution is altered, creating a dipole moment. In other words, the
external field separates positive and negative charges, creating an additional electric field called
the electric polarization, 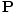 . The two fields are related by
(ε - ε0)
. The two fields are related by
(ε - ε0) . But |
. But |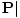 is also given by the product of the magnitude
of the charge, the displacement, and the total number of displaced charge per unit volume, N:
|
is also given by the product of the magnitude
of the charge, the displacement, and the total number of displaced charge per unit volume, N:
|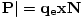 , for displaced electrons. Substituting the (time-averaged) value we found for x,
above, we have:
, for displaced electrons. Substituting the (time-averaged) value we found for x,
above, we have:
|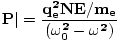 |
We can then write the relationship between
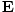 and
and 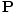 as ε = ε0 +
as ε = ε0 +  = ε0 + =
= ε0 + = 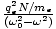 . Finally, n2 = ε/ε0 so we can
express the index of refraction as a function of the angular frequency of the light as:
. Finally, n2 = ε/ε0 so we can
express the index of refraction as a function of the angular frequency of the light as:
n2(σ) = 1 + 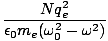 |
This is known as the dispersion equation. For frequencies above resonance (σ02 - σ2) < 0, the oscillators are about 180o with the driving electric field (see the discussion of phase-lag) , and n < 1. When the frequency is below resonance, (σ02 - σ2) > 0, the oscillation is in phase with the applied electric field and n > 1.
In general, index of refraction increases with frequency, and hence blue light refracts more through glass than red light. This situation is called normal dispersion. There are some cases of anomalous dispersion, usually close to resonance, where index of refraction decreases for higher frequencies.


 payment page
payment page



