Maxwell's Equations
The reason why the previous section developed the mathematics of waves was so that we
could apply it to the understanding of electromagnetic phenomena (to which light pertains). To begin we must
review Maxwell's equations which describe the relationship between electric and
magnetic fields. Here we will express the
equations in terms of the div, grad and curl of vector
calculus, however it is worth noting that the equations can also be expressed in integral form. For time-
varying electric and magnetic fields 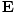 and
and 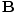 in free space:
in free space:
âàá×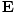 | = | (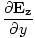 - - 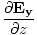 ) ) + ( + (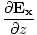 - -  ) ) + ( + (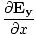 - - 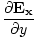 ) ) = - = - 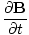 | |
âàá.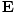 | = | 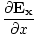 + + 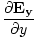 + + 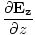 = 0 = 0 | |
âàá×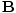 | = | (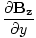 - - 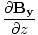 ) )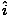 + ( + (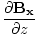 - - 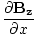 ) ) + ( + (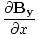 - -  ) )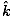 = μ0ε0 = μ0ε0 | |
âàá.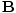 | = |  + + 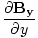 + + 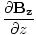 = 0 = 0 |
These equations tell us that the electric and magnetic fields are coupled: a time varying magnetic field will induce an electric field and a time varying electric field will induce a magnetic field. Moreover, the generated field is perpendicular to the original field. This suggests the transverse nature of electromagnetic waves. We can make use of the identity of vector calculus that âàá×(âàá×
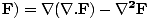 , where
, where 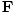 is some vector. Hence
âàá×(âàá×
is some vector. Hence
âàá×(âàá×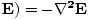 since âàá.
since âàá. , so:
, so:
âàá2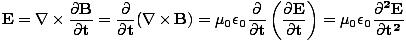 |
We can find a similar result for the magnetic field. From the definition of âàá2 (the Laplacian), we can write equations of the form:
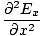 + + 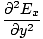 + + 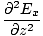 = μ0ε0 = μ0ε0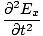 |
for every component of the electric and magnetic fields. But, comparing this to the differential wave equation we notice the above is just a wave equation in Ex, with the velocity equal to v =
 . Thus every component of the electric and magnetic field propagates
through space with this speed. Maxwell deduced this result and found it to be in close agreement with the
experimental value for the speed of light! This analysis remains one of the masterpieces of theoretical
physics.
. Thus every component of the electric and magnetic field propagates
through space with this speed. Maxwell deduced this result and found it to be in close agreement with the
experimental value for the speed of light! This analysis remains one of the masterpieces of theoretical
physics.
The propagation of light.
We can conclude from Maxwell's equations that light is in fact an oscillation of the electric and magnetic
fields that propagates through free space with velocity c = 1/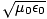 . Moreover, the
electric and magnetic fields are always mutually orthogonal and always in-phase. Since electric and
magnetic field have an associated energy, their propagation causes the transport of energy and momentum.
For this reason it is possible to calculate the energy density (energy per unit volume) of an electric or
magnetic field. In SI units these turn out to be:
. Moreover, the
electric and magnetic fields are always mutually orthogonal and always in-phase. Since electric and
magnetic field have an associated energy, their propagation causes the transport of energy and momentum.
For this reason it is possible to calculate the energy density (energy per unit volume) of an electric or
magnetic field. In SI units these turn out to be:
| uE | = 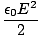 | ||
| uB | = 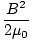 |
Since μ0 = 1/ε0c2 and |
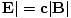 in SI units, then uB = uE.
This should not be a surprising result--it simply says the energy is divided equally between the electric and
magnetic fields. The total energy u is just u = uE + uB = 2uE = ε0E2 =
in SI units, then uB = uE.
This should not be a surprising result--it simply says the energy is divided equally between the electric and
magnetic fields. The total energy u is just u = uE + uB = 2uE = ε0E2 =  . Now the wave is propagating in a direction perpendicular to both the electric and
magnetic fields (this can be proved from Maxwell's equations) at speed c. Therefore, the power incident
on an area perpendicular to the direction of travel will have an amount of energy flow through it every
second of uc. This can be seen from the dimensions of energy/volume × distance/second = energy
per area per second. This is the incident power, S. Thus, S = uc =
. Now the wave is propagating in a direction perpendicular to both the electric and
magnetic fields (this can be proved from Maxwell's equations) at speed c. Therefore, the power incident
on an area perpendicular to the direction of travel will have an amount of energy flow through it every
second of uc. This can be seen from the dimensions of energy/volume × distance/second = energy
per area per second. This is the incident power, S. Thus, S = uc = 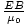 = c2ε0EB. We can express this more usefully as a vector
= c2ε0EB. We can express this more usefully as a vector 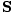 , perpendicular to
, perpendicular to 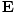 and
and
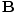 and normal to the surface across which the power per unit area is being calculated. This gives:
and normal to the surface across which the power per unit area is being calculated. This gives:
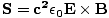 |
This is called the Poynting vector.
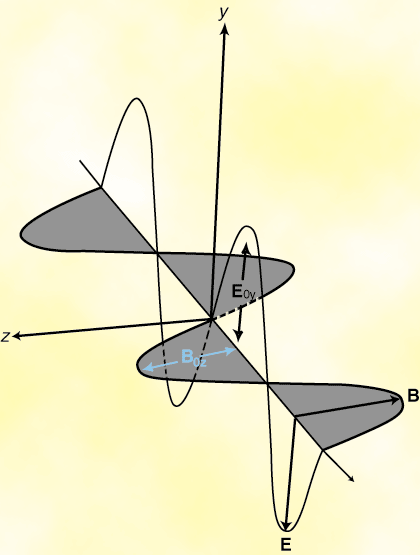
Thus light is a form of electromagnetic radiation, just like radiowaves, microwaves, infrared rays, X-rays, gamma rays and cosmic rays. It has frequencies in the range 3.84×1014 Hz to 7.69×1014 Hz, which corresponds to wavelengths of 780 to 390 nanometers.
Light as photons
It is important to realize that in contrast to the above wave description, Quantum Electrodynamics (QED) describes light and its interaction in terms of particles called photons. However, on a macroscopic level the particulate nature is not always evident and light can be treated as a wave. Indeed, according to quantum mechanics, all particles have wavelike properties. In other words, what we are really saying is that the electromagnetic field is quantized--light is emitted and absorbed in discrete units of energy E = hν. We call these chargeless, massless, particles photons. Photons can only exist at speed c and are totally indistinguishable from one another. This picture of light emerged from Planck's account of blackbody radiation in 1900 and Einstein's 1905 treatment of the photoelectric effect. These theories were very important in the rejection of classical mechanics and the formulation of wave mechanics that took place in 1920s. /PARGRAPH Photons are strange entities. They cannot be seen directly, but we can gain knowledge of them through their interactions when they are created or destroyed. This usually occurs when they are emitted or absorbed by electrons or other charged particles. The particle nature of light is confirmed by experiments such as Compton scattering that show how a photon colliding with a particle causes it to gain momentum and energy, with a consequent change in the frequency of the photon. In macroscopic situations, huge numbers of photons are involved and the electromagnetic wave is the time averaged result of the motion of many photons. If photons are incident on a screen, the intensity of light at a particular point is proportional to the probability of detecting a photon arriving at that location. QED develops a stochastic treatment of light phenomena which reduces to the classical (Maxwellian) result where large numbers of photons are involved.


 payment page
payment page



