Scattering and absorption
Up until now we have considered only light propagating in free space. Obviously, the subject of optics also concerns what happens inside matter. To understand this we need to examine what happens when a light wave, or a photon is incident on an atom. All the processes of transmission, reflection and refraction, are macroscopic manifestations of scattering effects on the atomic and subatomic levels.
When a photon (or light wave) encounters an atom, there are two possibilities: the atom may scatter the light, redirecting it without changing its frequency or energy, or it may absorb the light, using the energy to make a quantum jump into an excited energy state (more precisely, one of its electrons makes the jump). With absorption it is likely that the excitation energy will rapidly be transferred to atomic motion, via collisions, thus producing thermal energy before the atom decays back to the lower energy state re-emitting a photon. Scattering usually occurs only when the frequency of the photon is too small to cause a transition to any higher state. However, the electric and magnetic fields of the light drives the electron cloud of the atom into oscillation, causing it to re-radiate in all directions at that same frequency. We can imagine, on a simplistic level, the atom acting as point source of electromagnetic spherical waves. This process is elastic--no energy is lost to the atom. Importantly, the amount of scattering increases for frequencies closer to the resonant frequency for the particular atom. These resonant frequencies are those corresponding (via E = hν) to the exact, quantized differences between energy levels in an atom. Of course, a particular atom has many resonance frequencies, corresponding to jumps between different energy levels, and each one has a different likelihood of occurring. The gas atoms in air have resonant frequencies in the UV (Ultra-violet) range; thus air tends to scatter more blue light than red light. For sunlight coming laterally through the atmosphere, more blue light than red light is scattered towards the ground, so the sky looks blue! When the sun is low on the horizon, light passes through a greater thickness of air; the blue is scattered out and we see the left over red light coming directly along the line of sight to the sun, causing red sunsets.
However, this random scattering only occurs for media such as gases where the atoms are far apart and
randomly placed at distances far greater than the wavelength of the light. In dense, homogeneous media,
where the spacing of atoms is much less than the wavelength of the light, it turns out that very
little light gets scattered in the backwards direction or any direction perpendicular to the propagation of
the wave, but most gets propagated in the forward direction. This allows light to propagate through
dielectrics. This is somewhat surprising. Why shouldn't the light be scattered equally in all
directions? Consider , showing a regular array of very many closely spaced
atoms.

Fermat's Principle
Before we embark upon an analysis of reflection and refraction from the point of view of scattering light waves, it is worth exploring an alternative explanation for the propagation of light. Fermat's principle is a variational principle which states that:
The path taken by light going between any two points is the one that is traversed in the least time.
Indeed, by considering all possible paths for a light ray and choosing one which takes the least time, it is
possible to determine how a light ray will move. Consider a situation where a particle
moves from one medium to another.
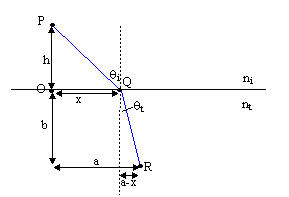
t = 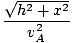 + + 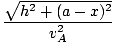 |
Minimizing time with respect to x:
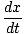 = =  + +  = 0 = 0 |
Rearranging this we find:
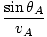 = = 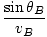 |
which is the law of refraction. In general, paths of minimum time are those paths which deviate little from their original value when the path is varied slightly (hence the word 'variational').
There is a good reason why light behaves in this way. After all, you may well ask, how does light know beforehand which path will take the least time? The answer lies in the variational nature of the principle; as stated, the path taken is the one for which adjacent paths correspond to very nearly the same time. Consider two points near the turning point of a smooth graph. Since the gradient is close to zero here a small x difference between the two points will only correspond to a small different y. However, for points located where the gradient is large in magnitude, small differences in x can correspond to large differences in y. Imagine for a moment that light takes all possible paths between two points. For points not close to the minimum path, adjacent paths will differ greatly in the amount of time required, thus the light along these paths will arrive at different times, and hence out-of-phase, interfering destructively. Light traversing the shortest-time path, however, will have adjacent paths that take nearly the same time, so light along these paths will arrive with in-phase, causing constructive interference. Thus light from all but this extremal path cancels out.


 payment page
payment page



