payment page
Problem :
A skater spins in the counterclockwise direction, as seen from above. In what direction does the vector representing the angular momentum of the skater point?
To find the direction of the angular momentum we use the right hand rule in the same way we used it for angular velocity. Thus, if we look down on the skater, and curl our fingers around in the counterclockwise direction, our thumb points towards us. Thus the angular momentum of the skater is pointing upwards.
Problem :
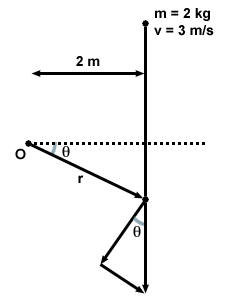
A particle moves in a straight line past a point O, as shown below. At which
point is the angular momentum maximum? If the distance between O and the line
is 2 m, and the object has a mass of 2 kg and a velocity of 3 m/s, what is the
maximum angular momentum of the particle with respect to O?
One might think that the maximum angular momentum will be when the object is
traveling in the tangential direction with respect to the radius. However,
notice that the radius is smallest at the point when the object is traveling in
the tangential direction. Since angular momentum varies with radius, it cannot
be maximal at this point. We will show that at all points, the angular momentum
of the particle is the same. Let's take another look at the figure, and
calculate the angular momentum at some arbitrary point, P:
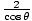from the
origin. In addition, the component of the velocity in the tangential direction
at P is given by 3 cosθ. Thus the angular momentum at this point is:
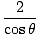= 12
Problem :
What is the angular momentum of a thin hoop of radius 2 m and mass 1 kg that is rotating at a velocity of 4 rad/s?
It can be easily shown, and has been established in other sections, that the moment of inertia of a thin hoop is simply MR2. Thus the angular momentum is easily calculable:
Problem :
Two particles travel in parallel directions, as shown below. What is the total
angular momentum of the system with respect to O?
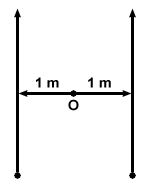
Quite simply, the total angular momentum is zero. At every point while the two particles are traveling, one particle moves in the clockwise direction with respect to O and one moves in the counterclockwise direction. Also, at every point, both particles have the same distance to the axis, and angle between the radius and the velocity of the particle. Thus the two particles always have equal and opposite angular momenta, and the total momentum of the system is zero.
Problem :
Many times a spinning top will not only spin about its axis, but precess about a vertical axis, meaning its point of contact with the ground remains the same, but the top swings around the vertical axis at an angle. What is the direction of the change in angular momentum in this situation? Where does the torque come from which causes this change in angular momentum?
We begin by drawing a diagram of the spinning top:
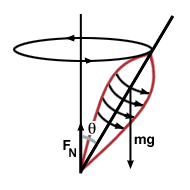
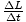. To find
the net torque on the top, we look at the forces acting upon the top. Where the
top is in contact with the ground, a normal force acts in the vertical
direction. Also, a gravitational force acts from the center of mass of the top.
Let's take our origin to be the point at which the top is in contact with
the ground. The gravitational force, then, exerts a torque of magnitude mg sinθ. Since the normal force acts at our origin, it exerts no torque. Thus
the net torque on the top has magnitude mg sinθ, and points
horizontally, into the page of our figure (by the right hand rule). Since a net
torque changes the angular momentum of an object, our change in momentum is in
the same direction, resulting in the precession motion of the top.
