Problem :
In an isolated system the moment of inertia of a rotating object is doubled. What happens to angular velocity of the object?
If the system is an isolated one, no net torque acts on the object. Thus the angular momentum of the object must remain constant. Since L = Iσ, if I is doubled, σ must be halved. Thus the final angular velocity is equal to one half its original value.
Problem :
A disk is spinning at a rate of 10 rad/s. A second disk of the same mass and shape, with no spin, is placed on top of the first disk. Friction acts between the two disks until both are eventually traveling at the same speed. What is the final angular velocity of the two disks?
We solve this problem using the principle of conservation on angular momentum. Initially the angular momentum of the system is entirely from the rotating disk: Lo = Iσ = 10I, where I is the moment of inertia of the rotating disk. When the second disk is added, it has the same moment of inertia as the first one. Thus If = 2I. With this information we can use conservation of angular momentum:
| Lo | = | Lf | |
| 10I | = | (2I)σf | |
| σf | = | 5 |
Thus the two disks have a final angular velocity of 5 rad/s, exactly half the initial velocity of the single disk. Notice that we got this answer without knowing either the mass of the disks or the moment of inertia of the disks.
Problem :
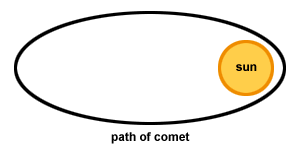
Explain, in terms of conservation of angular momentum, why comets speed up as they approach the sun.
Comets travel in wide elliptical paths, approaching the sun almost head on, then
quickly rotating around the sun, and travelling back into space, as shown in the
figure below:
Problem :
A particle attached to a string of length 2 m is given an initial velocity of 6 m/s. The string is attached to a peg and, as the particle rotates about the peg, the string winds around the peg. What length of string has wound around the peg when the velocity of the particle is 20 m/s?
As the string winds around the peg, the radius of rotation of the particle decreases, causing a decrease in the moment of inertia of the particle. The tension in the string acts in the radial direction, and thus does not exert a net force on the particle. Thus momentum is conserved and, as the moment of inertia of the particle decreases, its speed increases. Recall that v = σr. Thus the initial angular velocity of the particle is σo = v/r = 3 rad/s. In addition, the initial moment of inertia of the particle is Io = mR2 = 4m. We want to find r, the radius of the string when the particle has a speed of 20 m/s. At this point, the angular velocity of the particle is σf = v/r = 20/r and the moment of inertia is If = mr2. We have the initial and final conditions of the problem, and need only apply the conservation of angular momentum to find our value for r:
| Lo | = | Lf | |
| Ioσo | = | Ifσf | |
| (4m)3 | = | mr2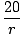 | |
| 12 | = | 20r | |
| r | = | .6 |
.4 meters of the string has wound around the peg when the velocity of the particle is 20 m/s.
Problem :
Two balls, one of mass 1 kg and one of mass 2 kg, are confined to move in a
circular track. They move at an equal velocity, v, in opposite directions on
the track and collide at a point. The two balls stick together. What is the
magnitude and direction of the velocity of the balls after the collision, in
terms of v?
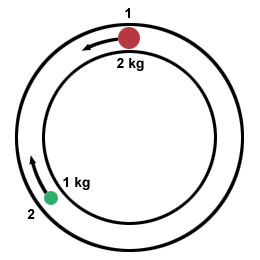
Just as we used conservation of linear momentum to solve linear collisions, we use conservation of angular momentum to solve angular collisions. Firstly, we define the positive direction as the counterclockwise direction. Thus the total momentum of the system is simply the sum of the individual angular momenta of the particles:
| l1 | = | mr2σ = 2r2 = 2rv = 2rv | |
| l2 | = | mr2σ = r = rv = rv |
Since the two particles move in opposite directions,
| Lo | = | L - f | |
| rv | = | 3rvf | |
| vf | = | v/3 |
Thus the final particle has a velocity a third of the initial velocity of each particle, and it moves in the counterclockwise direction.


 payment page
payment page



