Given a rotating body, we state that the body is made up of n single rotating
particles, each at a different radius from the axis of rotation. When each
particle is considered individually, we can see that each one does in
fact have a translational kinetic energy:
K =
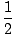 m1v12
m1v12 +
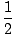 m2v22
m2v22 +
... 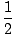 mnvn2
mnvn2
However, we also know from our relation between linear and angular variables
that
v = rσ. Substituting this expression in, we see that:
K =
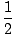 m1r12σ2
m1r12σ2 +
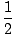 m2r22σ2
m2r22σ2 +
... 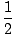 mnrn2σ2
mnrn2σ2
Since all particles are part of the same rigid body, we can factor our
σ2
:
K =
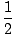
(
 mr2
mr2)
σ2
This sum, however, is simply our expression for a moment of inertia. Thus:
K = 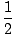 Iσ2 Iσ2 |
|
As we might expect, this equation is of the same form as our equation for linear
kinetic energy, but with
I substituted for
m, and
σ substituted for
v.
We now have rotational analogues for nearly all of our translational concepts.
The last rotational equation that we need to define is power.
Power
The equation for rotational power can be easily derived from the linear equation
for power. Recall that P = Fv is the equation that gives us instantaneous
power. Similarly, in the rotational case:
With the equation for rotational power we have generated rotational analogues to
every dynamic equation we derived in linear motion and completed our study of
rotational dynamics. To provide a summary of our results, the two sets of
equations, linear and rotational, are given below:
Linear Motion:
| F | = | ma |
|
| W | = | Fx |
|
| K | = | 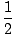 mv2 mv2 |
|
| P | = | Fv |
|
Rotational Motion:
| τ | = | Iα |
|
| W | = | τμ |
|
| K | = | 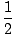 Iσ2 Iσ2 |
|
| P | = | τσ |
|
Equipped with these equations, we can now turn to the complicated case of
combined rotational and translational motion.