Problem :
Calculate the net torque exerted by F1 = 30 N and F2 = 50 N in the figure
below. You may assume that both forces act on a single rigid body.
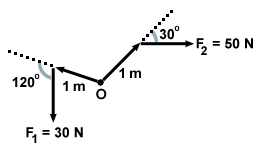
We begin be calculating the magnitude of each torque individually. Recall that τ = Fr sinθ. Thus τ1 = (30)(1)sin 120 = 26.0 N-m and τ2 = (50)(1)sin 30 = 25 N-m. As we can see from the figure, τ1 acts counterclockwise while τ2 acts clockwise. Thus the two torques act in opposite directions, and the net torque is thus 1 N-m in the counterclockwise direction.
Problem :
Two cylinders of the same mass and shape, one hollow and one solid, are set on a incline and allowed to roll down. Which cylinder will reach the bottom of the incline first? Why?
Since both cylinders have the same shape, they will experience the same forces, and thus the same net torque. Recall that τ = Iα. Thus the cylinder with the smaller moment of inertia will accelerate more quickly down the incline. Think of each cylinder as a collection of particles. The average radius of a particle in the solid cylinder is smaller than the hollow one, as most of the mass of the hollow one is concentrated at a larger radius. Since moment of inertia varies with r2, it is clear that the solid cylinder will have a smaller moment of inertia, and thus a larger angular acceleration. The solid cylinder will reach the bottom of the incline first.
Problem :
A simple pendulum of mass m on a string of radius r is displaced from vertical
by an angle θ, as shown below. What is the torque provided by gravity at
that point?
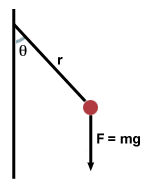
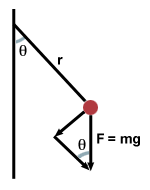
We begin by resolving the gravitational force into tangential and radial
components, as shown below:
Problem :
See the last problem. What is the angular acceleration of the pendulum at that point?
We already know the torque acting on the pendulum. Recall that τ = Iα. Thus, to find the angular acceleration we need to compute the moment of inertia of the pendulum. Fortunately, it is simple in this case. We can treat the mass on the pendulum as a single particle of mass m and radius r. Thus I = mr2. With this information we can solve for α:
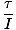 =
= 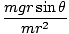 =
= 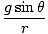
Problem :
A revolving door is common in office buildings. What is the magnitude of the
torque exerted on a revolving door of mass 100 kg if two people push on opposite
sides of the door with a force of 50 N at a distance of 1 m from the axis of the
door, as shown below? Also, the moment of inertia of a revolving door is given
by I = 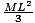 . Find the resultant angular acceleration assuming no
resistance.
. Find the resultant angular acceleration assuming no
resistance.
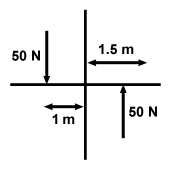
Although it looks like the forces are directed in opposite directions, and thus
cancel out, we must remember that we are working with angular motion here. In
fact, both forces point in the counterclockwise direction, and can be considered
to have the same magnitude and direction. In addition, they are both
perpendicular to the radial direction of the door, so the magnitude of the
torque by each one is given by: τ = Fr = (50 N)(1 m) = 50 N-m. As we stated,
the two forces act in the same direction, so the net torque is simply: 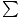 τ = 100 N-m.
τ = 100 N-m.
Next we have to calculate angular acceleration. We already know the net torque
and thus must find the moment of inertia. We are given the formula
I = 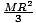 . We are given the mass, and from the figure we see that the
radius is simply 1.5 m. Thus:
. We are given the mass, and from the figure we see that the
radius is simply 1.5 m. Thus:
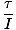 =
= 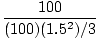 =
= 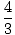 rad/s2
rad/s2


 payment page
payment page



