payment page
Two crucial concepts of Thermodynamics that spring directly from our work in the previous section are entropy and temperature. Here we define both and discuss how they relate to their more common definitions.
Entropy
We begin by revisiting the multiplicity function we looked at earlier. Let us modify the function slightly, so that instead of being a function of N and Nup, the total number of particles and the number of up magnets, let us generalize and let g now be a function of N and U, the energy of the system at hand. Now, this does not alter the definition at all; g still represents the number of states of the system with the same value of a particular variable, though in this case that variable is the energy U.
The entropy is defined as:
Notice that entropy is unitless. (Here, log is used to represent the natural logarithm, ln.) You might wonder why the entropy is defined this way. We will get at the answer via a short discussion of thermal equilibrium.
Suppose that we have two isolated thermal systems. The first has energy U1 and the second energy U2. Let the total energy between the two systems be constant, namely U. Then we can express the energy in the second system as U - U1. Furthermore, let the number of particles in the first system be N1 and that in the second N2, with the total number of particles N kept constant (so we can write N2 = N - N1).
Now suppose that the two systems are brought into thermal contact with each other, meaning that they can exchange energy but not number of particles. Then the total multiplicity function is given by:
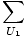g1(N1, U1)g2(N2, U - U1)
A good way to remember that the multiplicities come together in a product and not a sum is that they are fundamentally related to probabilities. Two separate probabilities governing two distinct events multiply together when we seek the probability of both events occurring. Since g = g1g2, we find using rules of logarithms that σ = σ1 + σ2. It is desirable to have the entropies of two systems add together upon contact, and this motivates the definition of entropy using the logarithm as above.
The combined system will redistribute energy between the two parts until g is at a maximum. At this point, any small change in U1 should yield no change in g by simple calculus. Some unenlightening algebra yields from this assertion that the condition for equilibrium is:
)N1 = (
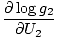)N2
The variables appearing as subscripts outside of the parentheses indicate that the partial derivatives inside the parentheses are taken at a constant value of that variable. Using our new definition of entropy as above, we can rewrite the equation as:
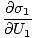)N1 = (
)N2
This formula is important to remember. When two systems in thermal contact achieve equilibrium, the rates of change of entropy with respect to energy in the two components are equal.
Temperature
We define the fundamental temperature τ as follows:
= (
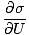)N
The temperature has units of energy. Notice that by defining the temperature this way, the condition for equilibrium between two systems in thermal contact given above become the more intuitive τ1 = τ2. The odd inverse definition is given to maintain a distinction of independent and dependent variables and will become clearer in Structure of Thermodynamics.
Conventional versus Fundamental Variables
Both terms, entropy and temperature, are often used to mean slightly different things than how we have defined them here. The conventional entropy, given by S, is defined as S = kBσ, where kB is the Boltzmann constant, experimentally given in SI units as:
The conventional temperature T is likewise defined, in units of kelvin:
Though T and S are more often used in fields such as chemistry, τ and σ are more fundamentally defined, and will be used exclusively here. However, should you need to use the other two, the conversions are simple; simply use the relations given above. Remember that the derivatives of the conventional and fundamental are not equivalent but differ by the Boltzmann constant. If you are working a problem and your answer is ridiculous, check to make sure you aren't missing a Boltzmann constant due to improper conversion.
