Problem :
A skier glides down a frictionless hill of 100 meters, the ascends another hill, of height 90 meters, as shown in the figure below. What is the speed of the skier when it reaches the top of the second hill?

The skier is in a conservative system, as the only force acting upon him is
gravity. Instead of calculating the work done over the curved hills, we can
construct an alternate path, because of the principle of path independence:
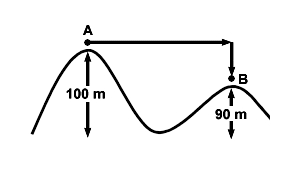
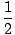 mvf2 = 10mg
mvf2 = 10mg
We can cancel the mass and solve for vf :
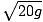 = 14m/s
= 14m/s
Problem :
What was the change in potential energy in the last problem, given that the mass of the skier is 50 kg?
Remember that ΔU = - W. We had calculated that the gravitational force exerted a work of 10mg during the entire trip. Thus the change in potential energy is simply the negative of this quantity: ΔU = - 10mg = - 500g = - 4900 Joules. The potential energy lost is converted into kinetic energy, accounting for the final velocity of the skier.
Problem :
What is the total energy of the mass-spring system shown below? The mass is
shown at its maximum displacement on the spring, 5 meters from the equilibrium
point.
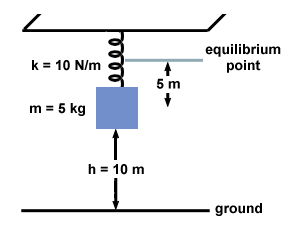
Here we have a system of two conservative forces, mass and gravity. Even if
there are more than one conservative force acting in a system, it is still a
conservative system. Thus potential energy is defined, and we can calculate the
total energy of the system. Since this quantity is constant, we may choose any
position for the mass that we like. In order to avoid calculating kinetic
energy, we choose a point at which the mass has no velocity: at its maximum
displacement, the position shown in the figure above. Also, since energy is
relative, we may choose our origin to be the equilibrium point of the spring, as
shown in the figure. Thus both the gravitational force and the spring force
contribute to the potential energy: UG = mgh = - 5mg = - 245 Joules. Also,
Us = 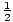 kx2 =
kx2 = 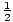 (10)(5)2 = 125 Joules. Thus the total potential
energy, and hence the total energy is the sum of these two quantities:
E = UG + Us = - 120 Joules. Remember that answers may vary on this problem. If we
had chosen a different origin for our calculations, we would have gotten a
different answer. Once we have chosen an origin, however, the answer for total
energy must remain constant.
(10)(5)2 = 125 Joules. Thus the total potential
energy, and hence the total energy is the sum of these two quantities:
E = UG + Us = - 120 Joules. Remember that answers may vary on this problem. If we
had chosen a different origin for our calculations, we would have gotten a
different answer. Once we have chosen an origin, however, the answer for total
energy must remain constant.
Problem :
A particle, under the influence of a conservative force, completes a circular path. What can be said about the change in potential energy of the particle after this journey?
We know that if the particle completes a closed path, the net work on the particle is zero. We already established through the Work-Energy Theorem that the total kinetic energy does not change. However, we also know that ΔU = - W. Since no work is done, the potential energy of the system does not change.
We can also answer this question in a more conceptual manner. We have defined potential energy as the energy of configuration of a system. If our particle returns to its initial position, the configuration of the system is the same, and must have the same potential energy.
Problem :
A pendulum with string of length 1 m is raised to an angle of 30o below the horizontal, as shown below, and then released. What is the velocity of the pendulum when it reaches the bottom of its swing?
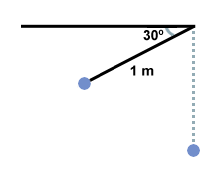
In this case there are two forces acting on the ball: gravity and tension from
the spring. The tension, however, always acts perpendicular to the motion of the
ball, thus contributing no work to the system. Thus the system is a conservative
one, with the only work being done by gravity. When the pendulum is elevated, it
has a potential energy, according to its height above its lowest position. We
can calculate this height:

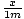 . Thus x = .5m and h = 1 - .5 = .5m. Now that we
have the initial height of the pendulum, we can calculate its gravitational
potential energy: UG = mgh = .5mg. All of this potential energy is converted into
kinetic energy at the final position of the pendulum, with a height of 0. Thus:
.5mg =
. Thus x = .5m and h = 1 - .5 = .5m. Now that we
have the initial height of the pendulum, we can calculate its gravitational
potential energy: UG = mgh = .5mg. All of this potential energy is converted into
kinetic energy at the final position of the pendulum, with a height of 0. Thus:
.5mg = 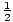 mv2. The masses cancel, and we can solve for v:
v =
mv2. The masses cancel, and we can solve for v:
v = 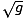 = 3.1m/s. Thus, when the pendulum reaches an angle of 90 with the
horizontal, it has a velocity of 3.1 m/s.
= 3.1m/s. Thus, when the pendulum reaches an angle of 90 with the
horizontal, it has a velocity of 3.1 m/s.


 payment page
payment page



