Previous Next

Work, though easily defined mathematically, takes some explanation to grasp conceptually. In order to build an understanding of the concept, we begin with the most simple situation, then generalize to come up with the common formula.

The Simple Case

Consider a particle moving in a straight line that is acted on by a constant force in the same direction as the motion of the particle. In this very simple case, the work is defined as the product of the force and the displacement of the particle. Unlike a situation in which you hold something in place, exerting a normal force, the crucial aspect to the concept of work is that it defines a constant force applied over a distance. If a force F acts on a particle over a distance x, then the work done is simply:

W = Fx    

Since w increases as x increases, given a constant force, the greater the distance during which that force acts on the particle, the more work is done. We can also see from this equation that work is a scalar quantity, rather than a vector one. Work is the product of the magnitudes of the force and the displacement, and direction is not taken into account.

What are the units of work? The work done by moving a 1 kg body a distance of 1 m is defined as a Joule. A joule, in terms of fundamental units, is easily calculated:

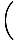
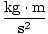
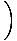W = Fx = (m) =

The joule is a multipurpose unit. It serves not only as a unit of work, but also of energy. Also, the joule is used beyond the realm of physics, in chemistry, or any other subject dealing with energy.

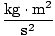
In dynamics we were able to define a force conceptually as a push or a pull. Such a concise definition is difficult to generate when dealing with work. To give a vague idea, we can describe work as a force applied over a distance. If a force is to do work, it must act on a particle while it moves; it cannot just cause it to move. For instance, when you kick a soccer ball, you do no work on the ball. Though you produce a great deal of motion, you have only instantaneous contact with the ball, and can do no work. On the other hand, if I pick the ball up and run with it, I do work on the ball: I am exerting a force over a certain distance. In technical jargon, the "point of application" of the force must move in order to do work. Now, with a conceptual understanding of work, we can move on to define it generally.

The General Case

In the last section we came up with a definition of work given that the force acted in the same direction as the displacement of the particle. How do we calculate work if this is not the case? We simply resolve the force into components parallel and perpendicular to the direction of displacement of the particle (see Vectors, Component Method). Only the force parallel to the displacement does work on the particle. Thus, if a force is applied at an angle θ to the displacement of the particle, the resulting work is defined by:

W = (F cosθ)x    

This new equation has similar form to the old equation, but provides a more complete description. If θ = 0, then cosθ = 1 and we have our first equation. Also, this equation ensures that it does not take into account any forces acting on a moving particle that do not do any work. Consider the normal force acting on a ball rolling across a horizontal floor. The normal force is perpendicular to the motion, implying that θ = 90 and cosθ = 0. Thus there is no work done on the ball by the normal force. In this sense, work can be seen as produced by any force that aids or hinders the motion of the particle. Stationary forces and forces perpendicular to the motion do not cause work.

Previous section Next page Definition of Work page 2

Take a Study Break