payment page
From the work done in the last section we can easily derive the principle of conservation of angular momentum. After we have established this principle, we will examine a few examples that illustrate the principle.
Principle of Conservation of Angular Momentum
Recall from the last section that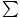 
τext = 
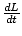. In light of
this equation, consider the special case of when there is no net torque acting
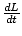on the system. In this case, must be zero, implying that the
total angular momentum of a system is constant. We can state this verbally:
If no net external torque acts on a system, the total angular momentum of the system remains constant.This statement describes the conservation of angular momentum. It is the third of the major conservation laws encountered in mechanics (along with the conservation of energy and of linear momentum).
There is one major difference between the conservation of linear momentum and conservation of angular momentum. In a system of particles, the total mass cannot change. However, the total moment of inertia can. If a set of particles decreases its radius of rotation, it also decreases its moment of inertia. Though angular momentum will be conserved under such circumstances, the angular velocity of the system might not be. We shall explore these concepts through some examples.
Examples of Conservation of Angular Momentum
Consider a spinning skater. A popular skating move involves beginning a spin with one's arms extended, then moving the arms closer to the body. This motion results in an increase of the speed with which the skater rotates increases. We shall examine why this is the case using our conservation law. When the skater's arms are extended, the moment of inertia of the skater is greater than when the arms are close to the body, since some of the skater's mass decreases the radius of rotation. Because we can consider the skater an isolated system, with no net external torque acting, when the moment of inertia of the skater decreases, the angular velocity increases, according to the equation L = Iσ.
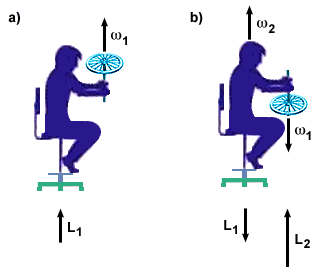
Another popular example of the conservation of angular momentum is that of a
person holding a spinning bicycle wheel on a rotating chair. The person then
turns over the bicycle wheel, causing it to rotate in an opposite direction, as
shown below.
Conclusion
We have now completed our study of angular momentum, and have likewise come to the end of our examination the mechanics of rotation. Since we have already examined the mechanics of linear motion, we can now describe basically any mechanical situation. The union of rotational and linear mechanics can account for almost any motion in the universe, from the motion of planets to projectiles.
