Converting between Individual Particles and Moles
Avogadro's Number provides the conversion factor for moving from number of particles to moles. There are 6.02×1023 formula units of particles in every mole of substance, with formula unit describing the substance we are looking at, whether it is a compound, molecule, atom, or ion. A formula unit is the smallest unit of a substance that still retains that substance's properties and is the simplest way to write the formula of the substance without coefficients. Some representative formula units are listed below.
- Compounds: Cu2S, NaCl
- Molecules: N2, H2
- Atoms: Fe, Na
- Ions: Na+(aq), Cl-(aq)
Moles = 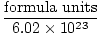 |
Converting between Solutions and Moles
Solutions are discussed in much greater detail in the series of Solutions SparkNotes. But it is possible, and fairly easy to convert between the measures of solution (molarity and molality) and moles.
Molarity is defined as the number of moles of solute divided by the number of liters of solvent. Rearranging the equation to solve for moles yields:
Moles = molarity × liters of solution
MolaLity is defined as the number of moles of solute divided by the number of kilograms of solvent. Rearranging the equation to solve for moles yields:
Moles = molality × kilograms of solution
Using the Mole Ratio to Calulate Yield
Before demonstrating how to calculate how much yield a reaction will produce, we must first explain what the mole ratio is.
The Mole Ratio
Let's look once again at our balanced demonstration reaction:
| 4Fe +3O2→2Fe2O3 |
The coefficients in front of iron, oxygen, and iron (III) oxide are ratios that govern the reaction; in other words, these numbers do not demand that the reaction can only take place with the presence of exactly 4 moles of iron and 3 moles of oxygen, producing 2 moles of iron (III) oxide. Instead, these numbers state the ratio of the reaction: the amount of iron and oxygen reaction together will follow a ratio of 4 to 3. The mole ratio describes exactly what its name suggests, the molar ratio at which a reaction will proceed. For example, 2 moles of Fe will react with 1.5 moles of O2 to yield 1 mole of Fe2O3. Alternatively, 20 moles of Fe will react with 15 moles of O2 to yield 10 moles of Fe2O3. Each of these examples of the reaction follow the 4:3:2 ratio described by the coefficients.
Now, with a balanced equation, the given units converted to moles, and our understanding of the mole ration, which will allow us to see the ratio of reactants to each other and to their product, we can calculate the yield of a reaction in moles. Step 4 demands that we be able to convert from moles to back to the units requested in a specific problem, but that only involves turning backwards the specific converstion factors described above.
Sample Problems
Problem: Given the following equation at STP:
| N2(g) + H2(g)→NH3(g) |
Determine what volume of H2(g) is needed to produce 224 L of NH3(g).
Solution:
br>
Step 1: Balance the equation.
| N2(g) + 3H2(g)→2NH3(g) |
Step 2: Convert the given quantity to moles. Note in this step, 22.4 L is on the denominator of the conversion factors since we want to convert from liters to moles. Remember your conversion factors must always be arranged so that the units cancel.
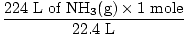 = 10 moles of NH3(g) = 10 moles of NH3(g) |
Step 3: mole ratio.
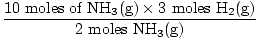 = 15 moles H2(g) = 15 moles H2(g) |
Step 4, convert to desired units:
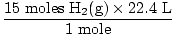 = 336 L H2(g) = 336 L H2(g) |
Now for a more challenging problem:
Given the following reaction:
| 2H2S(g) + O2(g)→SO2(g) + 2H2O(s) |
How many atoms of oxygen do I need in order to get 18 g of ice?
Solution
Step 1. The equation is partially balanced already, but let's finish the job.
| 2H2S(g) +3O2(g)→2SO2(g) + 2H2O(s) |
Step 2, convert to moles:
1 formula unit of H2O has 2 atoms of H and 1 atom of O
The atomic mass of H is 1 gram/mole
Atomic mass of O = 16 grams/mole
GFM of H2O(s) = 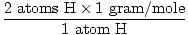 + + 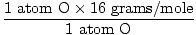 = 18 grams / mole = 18 grams / mole |
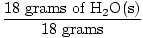 ×1 mole = 1 mole of H2O(s) ×1 mole = 1 mole of H2O(s) |
Step 3, mole ratio:
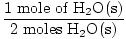 ×3 moles O2(g) = 1.5 moles O2(g) ×3 moles O2(g) = 1.5 moles O2(g) |
Step 4, convert to desired units:
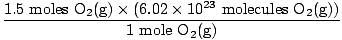 = 9.03×1023 molecules O2(g) = 9.03×1023 molecules O2(g) |
Is this the answer? No. The question asks for ATOMS of oxygen. There are two atoms of oxygen in each molecule of O2(g).
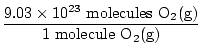 ×2 atoms O = 1.806×1024 atoms O ×2 atoms O = 1.806×1024 atoms O |
Now we're done. Note how important it was to write out not only your units, but what substance you're currently working with throughout the problem. Only a brief check was needed to ascertain if we were really answering the given question. Always check to make sure you have answered the correct question.


 payment page
payment page



