We have studied rotation on its own, and translation on its own, but
what happens when the two are combined? In this section we study the
case in which an object moves linearly, but in such a manner so that
the object's axis of rotation remains unchanged. If the axis of
rotation is changed, then our equations of rotation no longer apply.
Here, we will only study cases in which our equations of rotation work.
The most familiar example of combined rotational and translational
motion is a rolling wheel. While it is rolling, the axis of the wheel
remains the axis of rotation, and our equations apply.
Kinetic Energy of Combined Motion
One important principle of combined motion is that the kinetic
energies of translation and
rotation are additive. In other words, we can get the total kinetic
energy of a body by simply adding its rotational and translational
kinetic energy. We must be careful, however, because we never truly
defined translational kinetic energy for a rigid body (we only had a
definition for a single particle). We solve this problem by simply
using the velocity of the Center of Mass
of the object, which
provides
the velocity of the rigid body. Thus the total kinetic energy of a
particle is given by:
K = 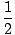 Mvcm2 + Mvcm2 + 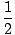 Iσ2 Iσ2 |
|
This equation can be quite useful. Say a rolling ball ascends a hill
until it stops. We can calculate the maximum height the ball will
reach by using the above equation and relating total kinetic energy to
potential energy.
Rolling Without Slippage
Many times we will know the velocity of an object, or its angular
velocity, but not both. Usually if this is the case the problem is
unsolvable. In the special case of rolling without slipping,
however, we can generate a solution.
Rolling without slipping is defined as the special case of combined
rotational and translational motion in which there is no relative
motion between the object and the surface with which it is in contact.
Examples of rolling without slipping include a car driving on a dry
road and a pool ball rolling across the table. In each case, the
surface can apply only static friction, since the object does not move
relative to the surface. Also, this frictional force does no work and
dissipates no energy. Thus an object rolling without slipping will
continue with the same linear and angular velocity, unless acted on by
another force.