Examples of Recursion: Recursion in Sorting

Note: This guide is not intended as a fully comprehensive guide to sorting, only a glimpse at how recursion can be used to effectively sort. For more information on the sorting algorithms described within (as well as other algorithms not mentioned), please see the SparkNote guide to sorting algorithms.

Recursive techniques can be utilized in sorting algorithms, allowing for the sorting of n elements in O(nlogn) time (compared with the O(n²) efficiency of bubble sort. Two such algorithms which will be examined here are Mergesort and Quicksort.

Mergesort

To discuss mergesort, we must first discuss the merge operation, the process of combining to sorted data sets into one sorted data set. The merge operation can be accomplished in O(n) time.

Given two sorted data sets to merge, we start at the beginning of each:

Figure %: Two ordered data sets to merge

We take the smallest element from the two we're comparing (these being the two elements at the front of the sets), and we move it into the new data set. This repetition is done until all of the elements have been moved, or until one of the lists is empty, at which point all of the elements in the non-empty list are moved to the new list, leaving them in the same order.

The following code implements the merge operation. It merges a1[] and a2[], and stores the merged list back into a1[] (therefore a1[] must be large enough to hold both lists):

void merge(int a1[], int a1_len, int a2[], int a2_len) { int joint_size; int a1_index, a2_index, joint_index; int *tempp; /* Create a temporary array */ joint_size = (a1_len + a2_len) * sizeof(int); tempp = (int *) malloc(joint_size); if (tempp == NULL) { printf("Unable to malloc space.\n"); return; } /* Do the merge pass */ joint_index = 0; a1_index = 0; a2_index = 0; while (a1_index < a1_len || a2_index < a2_len) { if (a1_index < a1_len && a2_index < a2_len) { if (a1[a1_index] < a2[a2_index]) { tempp[joint_index] = a1[a1_index]; } else { tempp[joint_index] = a2[a2_index]; } } else if (a1_index < a1_len) { tempp[joint_index] = a1[a1_index]; } else { tempp[joint_index] = a2[a2_index]; } } /* Copy the temporary back into the argument array */ for (joint_index = 0; joint_index < a1_len + a2_len; joint_index++) { a1[joint_index] = tempp[joint_index]; } /* Free the temporary array */ free(tempp); }

This merge operation is key to the mergesort algorithm.

Mergesort is a divide-and-conquer algorithm, meaning that it accomplishes its task by dividing up the data in order to better handle it. Mergesort has the following algorithm: split the list in half, sort each side, then merge the two sides together. See the recursive aspect? The second step of the mergesort algorithm is to sort each half. What algorithm might we use to sort each half of the set? In the spirit of recursion, we'll use mergesort.

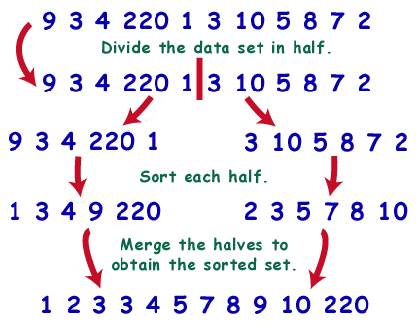
Figure %: Divide in half, sort each half, then merge the two halves.

void mergesort(int arr[], int n) { int a1_len; int a2_len; if (n <= 1) { return; } else { a1_len = n / 2; a2_len = n - a1_len; mergesort(arr, a1_len); mergesort(&arr[a1_len], a2_len); merge(arr, a1_len, &arr[a1_len], a2_len); } }

Just as with binary search, mergesort continually splits the data set in half, doing O(n) operations at each level of recursion. There are O(logn) splits of the data set. Therefore, mergesort() runs in O(nlogn) time, the provably best efficiency for a comparison-based sort.

Quicksort

Quicksort, an algorithm developed by C.A.R. Hoare in the 1960s, is one of the most efficient sorting algorithms; for a large, random data set, it is often considered to be the fastest sort. Like mergesort(), it is also a divide-and-conquer algorithm resulting in an average case running time of O(nlogn).

Like mergesort, quicksort partitions the data into two sets. The algorithm for quicksort is as follows: choose a pivot value (a value to which we'll compare the rest of the data in the set), put all values smaller than that pivot on one side of the set and all values greater than that pivot on the other side of the set, then sort each half. Again, we'll recursively sort each half of the data set using the same algorithm, quicksort.

Figure %: Partition the data by the pivot value, then sort each new set.

void swap_elements_ptr(int *a, int *b) { int temp = *a; *a = *b; *b = temp; } void quick_sort(int arr[], int n) { int num_equal, num_on_left, num_on_right; int val, *ip, *equalp, *less_thanp, *greater_thanp; if (n <= 1) return; val = arr[0]; equalp = arr; less_thanp = &arr[1]; greater_thanp = &arr[n - 1]; while (less_thanp <= greater_thanp) { if (*less_thanp == val) { equalp; swap_elements_ptr(less_thanp, equalp); less_thanp; } else if (*less_thanp > val) { swap_elements_ptr(less_thanp, greater_thanp); greater_thanp--; } else less_thanp; } less_thanp--; greater_thanp; for (ip = arr; ip <= equalp; ip++) { swap_elements_ptr(ip, less_thanp); less_thanp--; } num_equal = equalp - arr + 1; num_on_left = less_thanp - arr + 1; num_on_right = n - num_equal - num_on_left; quick_sort(arr, num_on_left); quick_sort(greater_thanp, num_on_right); }

Sometimes when the size of the partition gets small enough, a programmer will use another non-recursive sorting algorithm, like selection sort or bubble sort (see the SparkNote guide on sorting if you are unfamiliar with this sort), to sort the small sets; this often counters the inefficiency of many recursive calls.

void swap_elements_ptr(int *a, int *b) { int temp = *a; *a = *b; *b = temp; } void quick_sort(int arr[], int n) { int num_equal, num_on_left, num_on_right; int val, *ip, *equalp, *less_thanp, *greater_thanp; int i, j; /* Change base case to do bubblesort after threshold has been reached */ if (n <= 6) { for (i = 0; i < n; i) { for(j = 0; j < n-1; j) { if (arr[j] > arr[j+1]) { swap_elements_ptr(arr+j, arr+j+1); } } } return; } val = arr[0]; equalp = arr; less_thanp = &arr[1]; greater_thanp = &arr[n - 1]; while (less_thanp <= greater_thanp) { if (*less_thanp == val) { equalp; swap_elements_ptr(less_thanp, equalp); less_thanp; } else if (*less_thanp > val) { swap_elements_ptr(less_thanp, greater_thanp); greater_thanp--; } else less_thanp; } less_thanp--; greater_thanp; for (ip = arr; ip <= equalp; ip++) { swap_elements_ptr(ip, less_thanp); less_thanp--; } num_equal = equalp - arr + 1; num_on_left = less_thanp - arr + 1; num_on_right = n - num_equal - num_on_left; quick_sort(arr, num_on_left); quick_sort(greater_thanp, num_on_right); }

There are many variants of the basic quicksort algorithm, such as different methods for picking a pivot value (most of which are better than the one used above), methods for partitioning the data, different thresholds for stopping the recursion, etc. For more information, please refer to the SparkNote guide to sorting.

Previous section Next section