Problem : Someone on a moving train on the earth measures the speed of a meteor in space to be 5×106 m/s. Someone in outer space measures the speed to be 4×106 m/s. Who is right?
The first postulate says that neither observer is 'right' and that they are both right. Motion is relative, so any measurement made from an inertial reference frame is as good (or bad) as any other; both views have validity from their own points of view. Of course this assumes that one is considering the earth to be an inertial frame; this is roughly true but technically the rotation of the earth and the motion around the sun means than the earth is not an inertial frame (it is accelerating).Problem : Two spaceships are hurtling towards one another at a constant speed of 0.8c. When they are still 10 000 kilometers apart, one spaceship radios the other to warn them of the impending collision. How much time does it take for the radio wave to reach the other ship, as observed by someone on the receiving ship (assume that the spaceships move little in the time taken for the signal to travel between them)?
Despite the relative speed of the spaceship light still travels between them at speed c, according to our second postulate. Thus the time taken is just t = d /v = 10000/3×108 = 3.33×10-5 m/s.Problem : Consider the situation described in Section 1. If the flashes from the sources are observed to occur simultaneously by an observer standing on the ground (at rest relative to the sources), what is the time difference between the events according to an observer on a train speeding past at 0.15c, if that observer measures the distance between the sources to be 1 kilometer?
The distance between the sources is 1000 meters so here we have l = 500m. Then tr = =
= 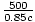 = 1.96×10-6 seconds, and tl =
= 1.96×10-6 seconds, and tl = 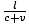 =
=  = 1.45×10-6 seconds. Thus the time difference is tr - tl = 5.12×10-7 seconds. Even at the immense speed of 45000 kilometers
per second, the time difference is hardly noticeable.
= 1.45×10-6 seconds. Thus the time difference is tr - tl = 5.12×10-7 seconds. Even at the immense speed of 45000 kilometers
per second, the time difference is hardly noticeable.
Problem : What if the scenario described in Section 1 is performed with baseballs (which travel at a constant speed b < c) instead of light pulses. Will the observers still disagree?
OA would still see the baseballs arrive simultaneously and conclude that they were thrown simultaneously. OB sees the baseball on the source on the right thrown with speed b - v and the baseball from the source on the left thrown with speed b + v. OB then calculates the speeds relative to the throwers as (b - v) + v = v on the left and (b + v) - v = v on the right. Thus OB too concludes that the baseballs arrive simultaneously. There is no disagreement; this comes about as a consequence of the weird properties of c.Problem : Consider again the scenario described in Section 1. Now consider changing the setup by placing only a single emitter at the center position (where OA was), and having two receivers placed where the sources formerly were. The source emits two signals, one in each direction (that is, one towards each receiver). An observer at rest with respect to the source and receivers concludes that the source emitted its two signals simultaneously. What does an observer traveling to the right at velocity v observe?
This situation is exactly analogous to the one described in Section 1. The only difference is that the light on the left of the center point is now traveling to the left, and the light to the right of the center point is moving to the right. Thus the moving observer concludes that the left- moving light takes a time tl = to reach the left receiver, and the right-moving light takes a time tr =
to reach the left receiver, and the right-moving light takes a time tr = 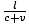 to reach the right receiver. Thus the 'left' and 'right'
times are swapped.
to reach the right receiver. Thus the 'left' and 'right'
times are swapped.


 payment page
payment page



