payment page
-
Length contraction
When an object is moving with constant velocity v with respect to an inertial observer its length in the direction of motion is contracted by a factor
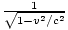. The dimensions of the object
perpendicular to the direction of motion are unaffected. This effect occurs at all velocities but only becomes
apparent at velocities close to c, the speed of light.
-
Time dilation
When an observer is moving with constant velocity v with respect to an inertial observer the clock of the moving observer appears to tick more slowly than that of the observer at rest. In other words, to the observer at rest the moving observer's time appears dilated. This means that the moving observers seconds are longer and hence they will measure less time between any two events by an amount proportional to
.
-
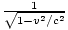Correspondence principle
We know that Newton's laws and classical mechanics do a very good job of explaining and predicting motion at everyday speeds. Thus we would hope that any new theory which we introduce would not completely overturn the classical results when low velocities are involved. Thus we insist that theories such as Special Relativity (or Quantum Mechanics) 'overlap' with the results of classical physics in the appropriate limits and regimes (such as when v < < c). In other words, the formulas of Special Relativity should reduce to the classical formulas in the limit v < < c. Only in this way can there be no contradiction between the theories (we wouldn't want them to contradict each other because we know classical mechanics does a good job for most purposes). This idea is called the correspondence principle.
-
Reference frame
A reference frame can be thought of as a set of coordinate axes (plus a clock) moving along with an object. Reference frame is used synonymously with 'rest frame', the reference frame in which an object is at rest (that is, stationary). The set of axes associated with a body or point provides a consistent way of looking at the world and making measurements; distances are measured according to the difference between ordinates and time measured by the number of ticks of the clock. Objects with different frames of reference will measure physical quantities, such as velocities, differently.
-
Ether
An incorporeal and undetectable medium through which physicists at the end of the nineteenth century believed light traveled. The ether was supposed to not only provide a medium for light but also to be a sort of absolute reference frame in which the laws of physics held exactly (especially Maxwell's equations) and the speed of light was c. Any reference frame in motion with respect to the ether should observe a variation in the speed of light with direction; Michelson and Morley's careful experiments could observe no such difference.
-
Relativity principle
One of the postulates or fundamental principles of Special Relativity that states that any two inertial reference frames are equivalent. This means that a measurement made in any inertial reference frame is just as valid as a measurement made in any other. Moreover, there is no such thing as an absolute reference frame and therefore no such thing as absolute motion; any motion can only be described as motion relative to some other inertial reference frame. Many of the results of Special Relativity can be deduced from this postulate.
-
Lorentz transformation
The equations that relate intervals in space and time (distance and time intervals measured in a particular frame) between two events in one frame to the space and time intervals in another frame moving with speed v in the x-direction with respect to the first frame. An 'event' is anything that can be given a particular spacetime coordinate: a location and a point in time. If the space and time intervals measured in the moving frame are the primed variables then the Lorentz transformations are:
Δx = γ(Δx' + vΔt') Δt = γ(Δt' + vΔx'/c2) Δy = Δy' , Δz = Δz'
-
Galilean transformation
The equations of classical mechanics which relate the time and distance between two events occurring in one frame to those another moving with speed v in the x-direction. If the primed coordinates correspond to the moving frame, then:
Δt = Δt' Δx = Δx' + vt' Δy = Δy' Δz = Δz'
-
Spacetime
In relativity it is often useful to think of space and time as a single entity or four-dimensional space, with three spatial dimensions and one dimension of time. When thought of as a four-dimensional coordinate system a Lorentz transformation between frames is equivalent to a rotation of these spacetime coordinates. The concept of spacetime neatly captures the interconnectedness of space and time in relativity.
-
Minkowski diagram
A diagram is drawn with an x-axis and a ct-axis at 90o. The path of any object through one dimensional space and time can be plotted on the diagram. A Lorentz transformation corresponds to a rotation of the axes to x' and ct' where the amount of rotation can be precisely calculated if the speed v is known. The path of an object remain the same as the coordinates are rotated underneath it, so a Minkowski diagram is useful for seeing schematically what the effect of a Lorentz transformation is.
-
Velocity addition formula
The Special Relativistic formula that relates the speed of an object in one frame to its speed in another. If an object is traveling with speed v in frame A that is moving with speed w with respect to frame B, the speed of the object, u, as measured in B is:
u =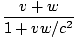 
-
Worldline
The path of a particle plotted on a Minkowski diagram is called its worldline.
Terms
Formulae
| For events occurring at the same place in A's frame: | tB = γtA. |
| For events occurring at the same time in A's frame: | lA = lB/γ. |
| The inverse Lorentz transformations are: |
|
