Problem : If observer Bill, who is on a train moving with speed 0.6c, waves to Julie at four second intervals as measured in Bill's frame, how long will Julie measure between waves?
Bill is in motion so we know that his seconds must be dilated (longer) with respect to Julie's seconds, by a factor γ. Thus Julie will measure more seconds between waves. What is γ?γ = 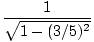 = 5/4 = 5/4 |
Thus Julie measures 5/4×4 = 5 seconds between waves.
Problem :
Bill and Julie are both now on identical trains. Bill's train is moving to the right with velocity (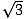 /2)c with respect to Julie's train. Julie measures her train to be 100 meters long. How long does Julie
measure Bill's train to be? How long does Bill measure Julie's train to be?
/2)c with respect to Julie's train. Julie measures her train to be 100 meters long. How long does Julie
measure Bill's train to be? How long does Bill measure Julie's train to be?
 = 2. Thus Julie will measure Bill's train to be 50
meters long. We know that Bill's train is identical, so because of the equivalence of frames and the
symmetry of the situation, we can say that Bill must measure his own train to be 100 meters long and Julie's
to be 50 meters long.
= 2. Thus Julie will measure Bill's train to be 50
meters long. We know that Bill's train is identical, so because of the equivalence of frames and the
symmetry of the situation, we can say that Bill must measure his own train to be 100 meters long and Julie's
to be 50 meters long.
Problem : What must be the average speed of a muon, a certain type of elementary particle, in order for it to travel 20 meters before it decays? The average rest lifetime of a muon is 2.60×10-8 seconds.
In the rest frame of the muon it has 2.60×10-8 seconds before it decays. In this time it must travel 20.0 meters in the lab frame. In the lab frame, the muon is measured to be travelling with speed v to the right (v is the speed we wish to find), so the muon sees the lab whizzing past to the left with speed v. For the muon, it sees the lab contracted by a factor γ (which corresponds to v), so in its frame it only has to travel a distance 20/γ in order to cover 20 meters as measured by an observer in the lab. Thus the velocity required is v =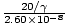 = 20
= 20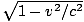 2.60×10-8. Solving this equation we find: v =
2.60×10-8. Solving this equation we find: v = 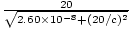 = 1.72×104 m/s.
= 1.72×104 m/s.
Problem :
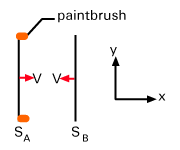
Consider the following scenario: two meter sticks, call the SA and SB are oriented parallel to the y
axis, some distance apart. The travel towards one another along the x-direction: that is, SA one
moves in the positive x-direction and SB moves in the negative x-direction (see ). SA has paint brushes on its ends, pointing towards SB such that if SB is
longer than SA, for example, it will leave paint marks on SB. Show that there is no length
contraction in the y-direction (that is, the sticks both appear 1 meter long to each other)? (Hint: assume
this is not the case and derive a contradiction).
Problem : Imagine a train going through a tunnel. The train and the tunnel both have length l in their own frame. The train moves through the tunnel with speed v. There is a bomb at the front of the train which is designed to explode when the front of the train passes out the far end of the tunnel. However, there is a disarming sensor located on the back of the train which will disarm the bomb just as the back of the train enters the near end of the tunnel. Will the bomb explode?
The answer is yes, the bomb will explode. In the frame of the train, it sees the tunnel as having length l /γ < l so the front of the train will pass out of the tunnel before the rear enters the tunnel (the train has length l in its own frame). One might argue that in the frame of the tunnel, the train appears contracted by the same factor and so in the tunnel frame the train is shorter than the tunnel by a factor γ, so the rear of the train will enter the tunnel before the front passes out, and the bomb will be disarmed. We appear to have a paradox. However, this second line of reasoning is false because it ignores the finite time that any disarming signal must take to move from the rear of the train to the bomb at the front. The fastest such a signal could move is at c. The bomb will be disarmed if and only if a signal traveling at c emitted from the rear of the tunnel at the instant the rear of the train passes, reaches the far end of the tunnel before the train does. Working still in the frame of the tunnel, the signal takes a time l /c, and the train takes a time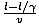 , since the front of the train is already a distance
l /γ (the length of the train) through the tunnel. For the bomb not to explode we need: l /c <
, since the front of the train is already a distance
l /γ (the length of the train) through the tunnel. For the bomb not to explode we need: l /c < 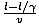 , which simplifies to
, which simplifies to 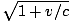 <
< 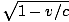 , which is clearly false. The bomb
explodes.
, which is clearly false. The bomb
explodes.


 payment page
payment page



