Problem : Show that the if we have tanhθ = v/c, the Lorentz transformations can be written as:


Δx = Δx'coshθ + cΔt'sinhθ    
Δct = Δx'sinhθ + cΔt'coshθ    

Since tanhθ = sinhθ/coshθ = v/c. The first transformation says (dropping the Δs): x = + . Now the γ factor is = = coshθ. Thus the first term becomes x'coshθ and the second vt'coshθ. But v = c tanhθ, so the second term becomes c tanhθt'cosθ = ct'sinhθ. Similarly, the second transformation says ct = + . The first term becomes ct'coshθ and the second vx'coshθ/c = x'tanhθcoshθ = x'sinhθ.

Problem : The Lorentz transformation expressed in the problem above may be represented in matrix form by:

=    

Show that is you apply one Lorentz Transformation with tanhθ1 = v1/c followed by another Lorentz transformation with tanhθ2 = v2/c, the result is also a Lorentz transformation with tanh(θ1 + θ2) = v.

To show this all we need to do is multiply the matrix with θ1s by the matrix with θ2s:

= =    

This is the Lorentz Transformation with v/c = tanh(θ1 + θ2) as desired. This is an important result: it means that when we transform from frame A to frame B and then from frame B to frame C, there exists a single transform of the same form which takes straight from A to C.

Problem : In the reference frame of an outside observer two particles move towards each other, both with velocity v. The angle between them is 2θ as shown in the figure below. What is the speed of one of the particles as viewed by the other?

Two particle approaching each other at an angle 2θ.

Consider the frame moving along with the particles along the dashed line midway between them. Call this frame F'. It has a speed v cosθ as given by the horizontal projection of the particles' speeds. The γ factor between F' and the frame of an outside observer is γ = . In F' the particle both move directly towards the fixed midpoint with speed u = γsinθ. The γ factor comes from the fact that clocks run slower in F' than in the outside observer's frame so the speed is greater in F' by a factor γ than it would be in the lab. We then use the velocity addition formula to find the speed of one particle with respect to another as:

w = =    

Problem : Show that the angle between the x and x' axes, as shown in , on a Minkowski diagram is given by tanθ2 = v/c. Also, determine the size of one unit on the x' axis.

The point (x', ct') = (1, 0) lies on the x' axis one unit from the origin. This Lorentz transforms to the point (x, ct) = (γ, vγ/c). The tangent of the angle θ2 is given by ct/x = = v/c. Hence tanθ2 = v/c. This point is a distance = γ1+v2/c2. This is the size of one unit on the x' axis.

Problem : Use a Minkowski diagram to solve the following problem. Frame F' moves at a speed v with respect to frame F along the x-direction. A 1-meter stick (as measured in F') lies along the x' axis, at rest in F'. An observer in F measures the length of the stick. What is the result?

Meter-stick in two different frames.
The solution to this problem is easy using Lorentz transformations, but we are not going to do it that way. We can choose the left end of the stick to be at the origin of F', and as such the worldlines of the ends of the stick are the ct' axis and another line parallel to it. The distance between these lines, as measured parallel to the x' axis must be 1 meter (shown as AC in ). But in terms of F, the segment AC has length (the length of one unit in F'). Someone in F measures the length by writing down the coordinates at the same time: for the sake of simplicity lets take t = 0. At this time the length of the stick is the length of the line segment AB. Now all is a matter of geometry. The x' angle is tilted by an angle θ, where tanθ = v/c. The length of CD is (AC)sinθ and the angle âà BCD = θ so BD = (CD)tanθ = (AC)sinθtanθ. Now, AB = AD - BD = (AC)cosθ - (AC)sinθtanθ = (AC)cosθ(1 - tan2θ) = (1 - v2/c2) = 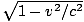. Thus the observer in F sees the stick shorter by 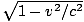, as we already knew.

Take a Study Break